Generate and plot XY data
Here I demo some of the trs_ tools I have for generating test data for XY transformation experiments.
Typical test location: /home/sco/sco/scohtm/scocodes/trs_/theta_solve/Work/test1 To generate and view the test data Note: * I simply composed the 6 points in file1.xy manually. * I generated the PointNames file with: % namelist 5 > PointNames % cat file1.xy # data -20 0 -10 0 5 0 15 0 25 0 % cat PointNames 1 2 3 4 5 % cat TRS.terms 0.0 0.0 N 1.0 30.0 0.0 0.0 % trs_apply file1 TRS.terms Y >file2 % cat file2 # data -17.321 10.000 -8.660 5.000 4.330 -2.500 12.990 -7.500 21.651 -12.500 % trs_2plot file1 file2 "Here is Plot Title" % trs_plot.py Style.file -30 30 -30 30 SHOWWith these steps I rotated the initial point set by 30 degrees (clockwise) and generated the plot below:
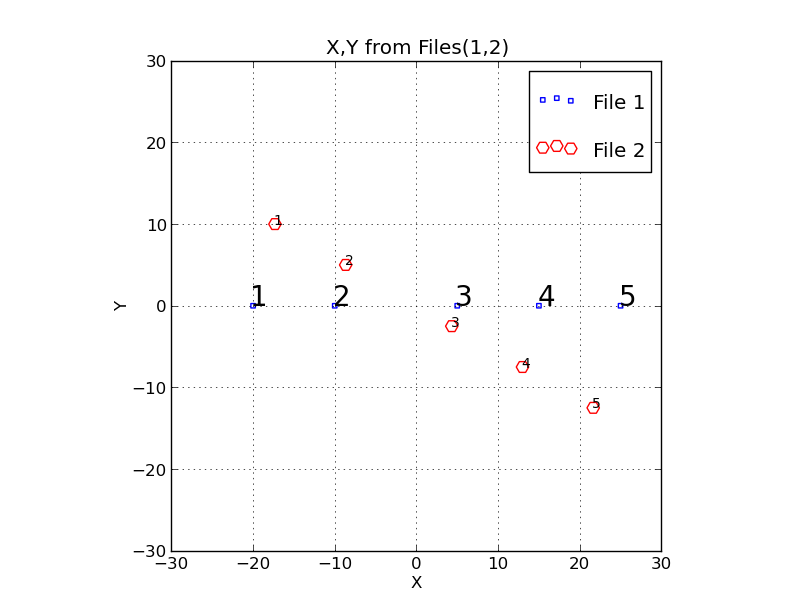 |
| Test data that has been rotated 30 gdegrees clockwise about the origin (0,0). |
Some quick conclusions
The plot above demonstrates well a major problem I have been having. I usually just fit a rotation using two linearly indpendent equations (as in xy_tranrot_fit.sh):
Equation:
The set2 coordinates are transformed to the set1 system via
the relations:
Xset1 = avals(1) + avals(2)*Xset2 + avals(3)*Yset2
Yset1 = avals(4) + avals(5)*Xset2 + avals(6)*Yset2
If the points are translated and scaled to a unform scale, the
coefficients above related directly to the rotation angle, theta:
X_t = x*cos(theta) + y*sin(theta)
Y_t = y*cos(theta) - x*sin(theta)
However, in the above case, where all of the points lie along a single
line, this approach fails, even for perfect (noiseless) data. I need a
morre robust approach. I had hope to using my two LS fits to get the
coefficients and then derive theta directly. This does not always work
(as above!). Next, I tried to solve theta directly using pairs of points.
I hit the classic problem of sin,cos asymmetry. In other words, I was not
always able to find a consistent angle. Hence, I swallowed my pride and
codes up a bonehead approach. This routine (trs_rotatedet.sh) always uses
a clockwise (CW) rotation direction to transform the Set2 XY to the XY Set1
system:
% trs_rotatedet.sh Usage: trs_rotatedet.sh file1.xy file2.xy arg1 - file1 of input X,Y (with # data header) arg2 - file2 of input X,Y (with # data header) Ratio computed is file1/file2The job now is to test this code by generating test sets with noise and various conditions: different rotation angle, different numbers of points, etc... After that, I'll embed trs_rotatedet.sh into a script that performs the full transformation derivation using trs_ routines.
Different angles with noiseless data.
I want to generate XY values, apply rotation with no noise and then test
whether trs_rotatedet.sh returns the correct rotation angle. I have written
a simple script named TRS_test1 (sreporduced below) to perform this and test that
the rotation solutions are valid at many different angles. The script generated
(noisless) rotated data. The rotation angle is derived, the data transformed
back to the original system and a plot of the two coordinate sets is built.
An example of a large rotation is shown below.
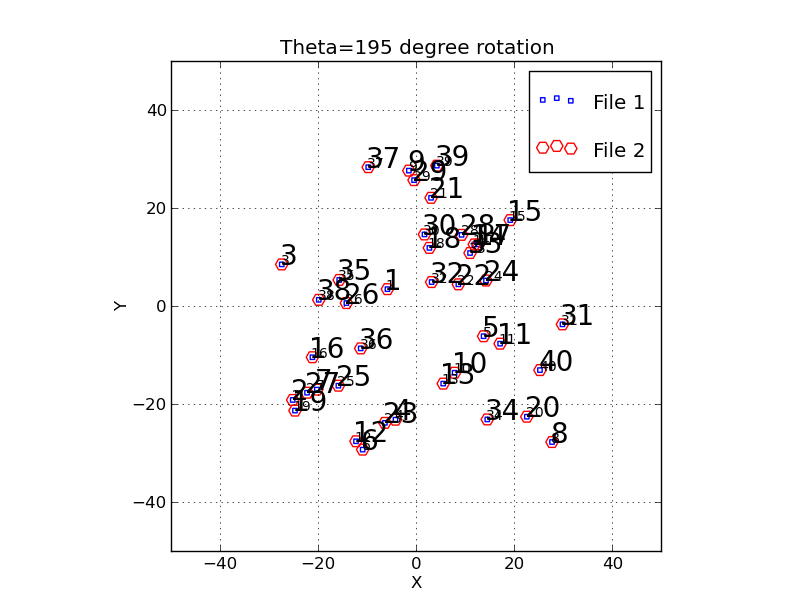 |
| The forty blue points above were generated in TRS_test1 with a random distribution. A rotation of 195 degrees in the clockwise direction was applied. The rotation solver (trs_rotatedet.sh) was used the derive the rotation, and the values used to transform the rotated set back to the original coordiant set. These transformed coordinates (File 2 in the legend) are plotted above as red circles. As can be seen, the match is very good. Although this routine uses a very brute-force (i.e. bonehead) approach, the code runs very quickly and produces relaible results. |
For completense I reproduce TRS_test1 below:
The TRS_test1 source code and test runs are stored in: /home/sco/sco/scohtm/scocodes/trs_/theta_solve/Work/test1 #!/bin/bash # Generate X,Y dat and rotate it # Check command line args if [ -z "$1" ] then printf 'Usage: TRS_test1 20 30.0 \"My XY Data\" \n' printf "arg1 - number of points \n" printf "arg2 - rotation in degrees \n" printf "arg3 - plot title in quotes \n" exit fi npoints="$1" theta="$2" title="$3" printf "Title in TRS_test1 = \"$title\" \n" # Genterate names namelist $npoints > PointNames #------------------------------------------------- # Make the XY data file # Generate the X data gen_noise.sh unif $npoints -30.0 30.0 > temp1 colget.py temp1 1 X N # Genetrate the Y data sleep 2 date > seed gen_noise.sh unif $npoints -30.0 30.0 > temp2 colget.py temp2 1 Y N printf "# Original data\n# data\n" > file1 paste X Y >> file1 \rm -f temp1 temp2 seed X Y head.lines ttt #------------------------------------------------- #------------------------------------------------- # Rotate printf "0.0 0.0 N 1.0 $theta 0.0 0.0" > TRS.terms trs_apply file1 TRS.terms Y \"$title\" >file2 #------------------------------------------------- #------------------------------------------------- # prep for a plot #trs_2plot file1 file2 "$title" #------------------------------------------------- #------------------------------------------------- # Solve, tranform and plot trs_rotatedet.sh file1 file2 > rot.terms read thetaS err rmspix nump < rot.terms printf "0.0 0.0 N 1.0 $thetaS 0.0 0.0\n" > trs.solve trs_apply file2 trs.solve Y > file3 trs_2plot file1 file3 "$title" #------------------------------------------------- # Clean up the joint \rm -f head.lines trs_apply.explain TRS.terms XF xy.FINAL xy.step1_translate \rm -f xy.step2_reflect xy.step3_scale xy.step4_rotate xy.step5_translate YF \rm -f trs_rotatedet.out1 trs.solvei rot.termsI have tested that all rotation quadrants are correctly treated. I used up to 200 points per fit. All of the fits run in a less than a second (excluding the 4 second sleep I use between the generation of random number sets).
Adding some noise to the tests.
Most applications of trs_rotatedet.sh will involve X,Y values with errors. Hence, I expanded on the simple script in the prvious section to added gaussian noise to the rotated set of coordinates. Below I record the script (TRS_test2) and a tabulation of results from TRS_test2.
The TRS_test2 source code and test runs are stored in:
/home/sco/sco/scohtm/scocodes/trs_/theta_solve/Work/test2
#!/bin/bash
# Generate X,Y dat and rotate it
# Check command line args
if [ -z "$1" ]
then
printf 'Usage: TRS_test2 20 30.0 0.3 0.55 \"My XY Data\" \n'
printf "arg1 - number of points \n"
printf "arg2 - rotation in degrees \n"
printf "arg3 - sigma of gaussian noise on transformed X values\n"
printf "arg4 - sigma of gaussian noise on transformed Y values\n"
printf "arg5 - plot title in quotes \n"
exit
fi
npoints="$1"
theta="$2"
sigx="$3"
sigy="$4"
title="$5"
printf "TRS_test1 = \"$title\" \n"
# Generate names
namelist $npoints > PointNames
#-------------------------------------------------
# Make the XY data file
# Generate the X data
gen_noise.sh unif $npoints -30.0 30.0 > temp1
colget.py temp1 1 X N
# Genetrate the Y data
sleep 2
date > seed
gen_noise.sh unif $npoints -30.0 30.0 > temp2
colget.py temp2 1 Y N
printf "# Original data\n# data\n" > file1
paste X Y >> file1
\rm -f temp1 temp2 seed X Y head.lines ttt
#-------------------------------------------------
#-------------------------------------------------
# Rotate
printf "0.0 0.0 N 1.0 $theta 0.0 0.0" > TRS.terms
trs_apply file1 TRS.terms Y \"$title\" >file2
# prep for a plot
#trs_2plot file1 file2 "$title"
#-------------------------------------------------
#-------------------------------------------------
# Generate noise and add to rthe rotated data
# Handle the X axis
gen_noise.sh gaus $npoints 0.0 $sigx > sigma.valX
colget.py file2 1 Xval Y
oned_imarith.sh Xval + sigma.valX fileX_nohead N
sleep 2
date >seed
# Handle the Y axis
gen_noise.sh gaus $npoints 0.0 $sigy > sigma.valY
colget.py file2 2 Yval Y
oned_imarith.sh Yval + sigma.valY fileY_nohead N
# build a full XY file with header info
printf "# file1 data rotated by $theta degrees\n" > file2.nooisy
printf "# Noise on X axis = $sigx\n" >> file2.nooisy
printf "# Noise on Y axis = $sigy\n" >> file2.nooisy
printf "# data\n" >> file2.nooisy
paste fileX_nohead fileY_nohead >> file2.nooisy
# rename the files
mv file2 file2_original
mv file2.nooisy file2
#-------------------------------------------------
#-------------------------------------------------
# Solve, tranform and plot
trs_rotatedet.sh file1 file2 > rot.terms
read thetaS err rmspix nump < rot.terms
printf "0.0 0.0 N 1.0 $thetaS 0.0 0.0\n" > trs.solve
trs_apply file2 trs.solve Y > file3
trs_2plot file1 file3 "$title"
#-------------------------------------------------
#-----------------------------------------------------------------------------
# Compute residuals
xy_tranrot_res.sh file1 file3 Y > XY.res
read Xrms Yrms Nres < XY.res
printf "\n"
printf "Comparing the Original(file1) and Back-Transformed(file3) XY: \n"
printf "Input rotation angle (degrres) = $theta \n"
printf "Input X,Y noise levels = $sigx $sigy\n"
printf "RMS of X residuals (file1-file3) = $Xrms\n"
printf "RMS of Y residuals (file1-file3) = $Yrms\n"
printf "Number of ressidals points used = $Nres\n"
#-----------------------------------------------------------------------------
# Write to a file
printf "$theta $err $npoints $sigx $sigy $Xrms $Yrms\n" >> TRS_test2.Results
# Clean up the joint
\rm -f head.lines trs_apply.explain TRS.terms XF xy.FINAL xy.step1_translate
\rm -f xy.step2_reflect xy.step3_scale xy.step4_rotate xy.step5_translate YF
\rm -f trs_rotatedet.out1 trs.solvei rot.terms
-------------------------------------------------------------------------------
TRS_test2 Results
=================
Theta m.e Npoints sigX sigY Xrms Yrms
60.0 0.3622 30 0.3 0.5 0.452 0.404
90.0 0.2229 30 0.3 0.5 0.467 0.281
120.0 0.2531 30 0.3 0.5 0.426 0.386
170.0 0.2171 30 0.3 0.5 0.311 0.455
220.0 0.2986 30 0.3 0.5 0.395 0.413
270.0 0.1560 30 0.3 0.5 0.496 0.301
290.0 0.2276 30 0.3 0.5 0.537 0.305
300.0 0.3178 30 0.3 0.5 0.444 0.401
60.0 0.3238 30 0.1 0.5 0.402 0.243
300.0 0.4996 30 0.5 0.5 0.491 0.467
300.0 0.7184 30 1.0 0.5 0.693 0.923
300.0 1.8701 30 3.0 0.5 1.498 2.660
300.0 2.8264 30 6.0 0.5 2.621 5.244
60.0 0.1670 30 0.5 0.1 0.268 0.441
300.0 0.2519 30 0.5 0.5 0.528 0.432
300.0 0.3790 30 0.5 1.0 0.843 0.591
300.0 1.7387 30 0.5 3.0 2.982 1.859
300.0 2.3951 30 0.5 6.0 5.277 2.976
70.0 0.9620 30 1.0 1.5 1.434 0.859
70.0 0.5065 90 1.0 1.5 1.439 1.049
70.0 0.3578 150 1.0 1.5 1.463 1.072
70.0 1.4537 200 1.0 1.5 1.394 0.974
70.0 0.2269 500 1.0 1.5 1.504 1.021
70.0 0.3158 800 1.0 1.5 1.465 1.016
Back to calling page