What is parallactic angle? This subject comes up continually in HET discussions. We need a concise description! Actually, the spherical trig equations are not that difficult, but it is important to clarify the angle conventions used upstream in the calculations. In this little webdoc I'll try to make this clear to my satisfaction.

1. A basic description and equations.
2. The working equations for HET.
3. A simple approach: bonehead all the way!
4. How to compute parallactic angle (Q).
5. What HET does (not really q!).

You can read a good description of the parallactic angle here . I took the very nice figure shown below from that page:

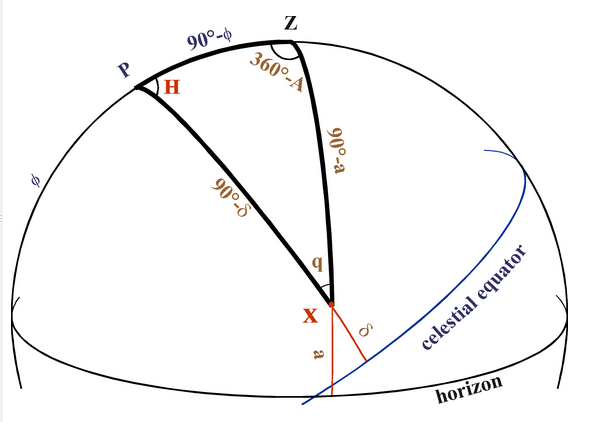To convert between the horizontal and equatorial coordinates for an object X, we use a spherical triangle often called "The" Astronomical Triangle: XPZ, where Z is the zenith (top of the sky), P is the North Celestial Pole, and X is the object we are pointing at on the celestial sphere. Recall that a great circle (GC) on the celestial sphere (CS) has a circumference that is the maximum circumference for the idealized sphere. So, the equator IS a GC, but a circle of constant declination (except on the equator!) IS NOT a GC. I am not going to the trouble of making greek letter here, so I refer to the latitude (denoted with a greek phi) as phi, and I refer to the declination (denoted with a greek delta) as DEC. a = altitude (angle directly above the horizon) phi = observer's latitude DEC = Declination of the target object. The sides of the triangle: PZ is the observer's co-latitude = 90deg - phi. ZX is the zenith distance of X = 90deg - a. PX is the North Polar Distance of X = 90deg - DEC. The angles of the triangle: The angle at P is H, the local Hour Angle of X. The angle at Z is 360deg-A, where A is the azimuth of X. The angle at X is q, the parallactic angle.

1. The GC that contains the TARGET (X) and the ZENITH (Z).
2. The GC that contains the TARGET (X) and the POLE (P).

As far as I can tell, the basic equations for pointing the HET are described in Frank Ray's 1994 "HET Technical Report #42". All HET TCS (Telescope Control System) seem to have their genesis there. This is an important paper, and I should have a link to it. Unfortunately, the PDF for this work is very large, and I do not carry it around in my SCO personal notes for that reason. There should be a WEB LINK for getting this report!!!

I did receive some formulae that may be helpful at some stage, but there may be some misunderstanding of angle conventions that remain (i.e. what angles are 0-360, and which use a 0-180 convention with an associated sign?). The important reasons for including these code snippets is that somewhere here are the equations that the HET TCS uses (or used) to compute parallactic angle.

 


 From Matt (02/20/2015) 
===========================================================================
So it should be a constant offset between the parallactic angle and the 
position angle not a constant offset between the Az and position angle.

There is some web code that computes this:
/home/het/astronomer/HETweb_Programs/Instruments

rho.c:
#define R2D 57.29577958      /* degrees per radian */
#define Q 0.417863           /* sin alt * sin latitude */       Not alt!
#define P 0.493336           /* cos alt * cos latitude */       Not alt!
#define telangle          55.0
#define latitude          30.6716667

 
The explanations of Q,P above are INCORRECT 
They should read: 
 
#define Q 0.417863           /* sin telangle * sin latitude */
                                 0.81915     *     0.51012         =  0.417864          

#define P 0.493336           /* cos telangle * cos latitude */     
                                 0.57358     *     0.860105        =  0.493339

DEC2 = DEC2/R2D;
az = 1/P*(sin(DEC2)-Q);
tde = P*cos(az/R2D) + Q ;
tde = atan2(tde,sqrt(1-tde*tde)) * R2D;
h = (cos(telangle/R2D)*sin(az/R2D))/-cos(tde/R2D);
h = atan2(h,sqrt(1-h*h))*R2D;
   parang=cos(h/R2D)*cos(az/R2D)+sin(h/R2D)*sin(az/R2D)*sin(latitude/R2D);
parang = atan2(sqrt(1-parang*parang),parang)*R2D;

Then if you are working in the West you have to do a 360-parang
===========================================================================



 From Jim  (02/04/2015) 
===========================================================================
Steve,
Here is how the Tcs calculates paralactic angle.  Telecentric azimuth 
is the structure azimuth and telecentric elevation is basically 
55 degrees.  Our latitude is 30:40:53.17

  Intermediate variables.
     P = cos( Telecentric Elevation ) * cos( Latitude )
     Q = sin( Telecentric Elevation ) * sin( Latitude )

These parameters are dependent only on the Az/El of the telecentric axis.

     Tde: Telecentric Declination
      H0: Telecentric Hour Angle 

     Tde = asin( P * cos( Telecentric Azimuth ) + Q )

     H0  = asin(-cos( Telecentric Elevation ) * sin( Telecentric Azimuth ) / cos( Tde ) )


      Pa Paralactic Angle = acos( cos( H0 ) * cos( Telecentric Azimuth ) 
           + sin( H0 ) * sin( Telecentric Azimuth ) * sin( Latitude ) )

Best wishes,
Jim
===========================================================================

Viewing the nice figure above, it becomes clear that the parallactic angle (q in our figure) really depends on three quantities: the hour angle of the target, the Declination of the target, and the Latitude that your are observing from. The code snippets above are nice, but certain angle conventions are not clear (to me) and much of the code is built for the HET. In surfing around, I found references to how this is done in python with astropy. Again a lot of the angle conventions (units, signs, ranges, ...) are buried in the calls to the astropy routines, and trying to follow the extremely poor astropy coordinates/units documentation does not get us very far. However, the python code below does, in fact, reveal the equations you need (in the comments!) to compute q given (HA,Dec,Lat). I'll code this up (in an OTW environment) so that I understand the numerics (units, signs, precision) and produce a simple command line tool that does the calculation.

 
the URL where I read about this:
https://github.com/brandon-rhodes/pyephem/issues/24

The not-so-clear Python code (using astropy): 
from math import sin, cos, tan, atan
import astropy.units as u
import ephem

##-------------------------------------------------------------------------
## Parallactic Angle
##-------------------------------------------------------------------------
def ParallacticAngle(HA, dec, lat):
    '''
    Function to calcualte the parallactic angle.

    Equations from:
    "A treatise on spherical astronomy" By Sir Robert Stawell Ball
    (p. 91, as viewed on Google Books)


    sin(eta)*sin(z) = cos(lat)*sin(HA)
    cos(eta)*sin(z) = sin(lat)*cos(dec) - cos(lat)*sin(dec)*cos(HA)


    Where eta is the parallactic angle, z is the zenith angle, lat is the
    observer's latitude, dec is the declination, and HA is the hour angle.

    thus:

    tan(eta) = cos(lat)*sin(HA) / (sin(lat)*cos(dec)-cos(lat)*sin(dec)*cos(HA))
    '''
    assert type(HA) == u.quantity.Quantity
    assert type(dec) == u.quantity.Quantity
    assert type(lat) == u.quantity.Quantity
    HArad = HA.to(u.radian).value
    latrad = lat.to(u.radian).value
    decrad = dec.to(u.radian).value
    taneta = cos(latrad)*sin(HArad) / (sin(latrad)*cos(decrad) - cos(latrad)*sin(decrad)*cos(HArad))
    return atan(taneta)*u.radian

The bonehead aspect of this is how I will now go about confirming that my (eventual) calculation of parallactic angle is correct. To do this, I collect FITS header information from LRS images stored on mcs. I used the gethead routine in a script to run something like:

 
gethead blah.fits DATE-OBS UT ST RA DEC AZIMUTH HA ZD PARANGLE >> HET.LRS_INFO

 
$scohtm/het+virus/het_upgrade/parallactic_angle/work_stuff/info.py

 
% wc -l list.*
  38 list.AZIMUTH
  38 list.DATE-OBS
  38 list.DEC
  38 list.HA
  38 list.PARANGLE
  38 list.RA
  38 list.ST
  38 list.UT
  38 list.ZD

From the exercise above I had a TCS-produced set of values relating sky coordinates and time. My goal for the purposes of processing CAT data is to compute the parallactic angle, Q, for any CAT image. As the CAT image headers contain only the UT data and time that they were taken (the isot-format date string in the astropy Time module terminology), I also needed some tools that allowed me to compute things like sidereal time (ST) and hour angle (HA). I had to construct a table of sky coordinates (RA,DEC) for the CAT image positions. This table of RA,DEC positions was collected from my README notes in the CAT data subdirectories. 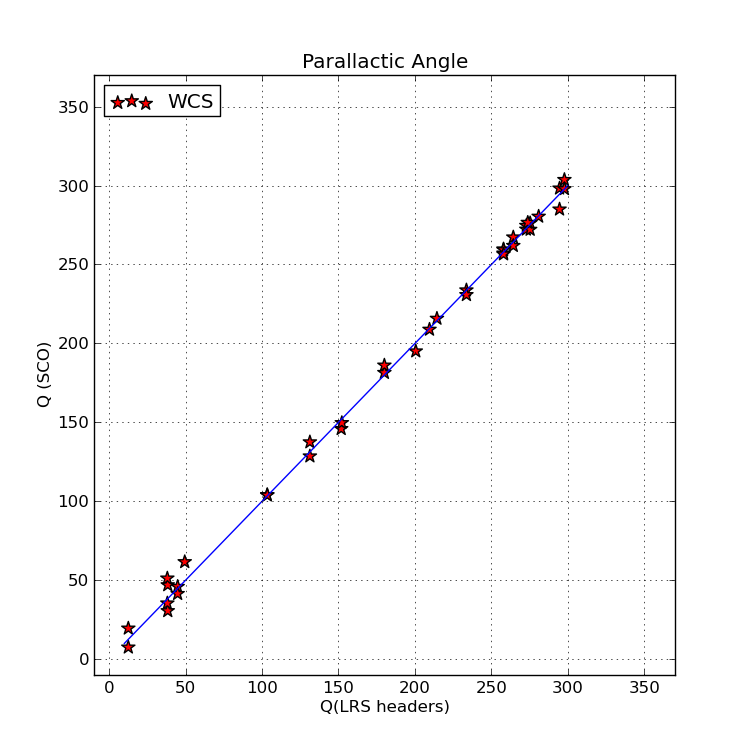Using the LRS data described above, I was able to confirm my parallactic angle calculations, and results from my 38 LRS test cases are shown below:

Parallactic angle (Q) values computed with the script Cal_q.sh (which uses the bash shell script mcd_parallactic_angle) are plotted on the Y axis. The corresponding parallactic angle values from the LRS images headers (contained in the file list.PARANGLE) are plotted on the X axis. The blue line has a slope of unity. The small amount of scatter is the result of the LRS value being referred to the center of the HET track (as I believe this is the angle that the rotator maintains during an HET observation).

The HET really uses a "Parallactic Direction", and the real parallactic angle. Also, the value is always computed for the center of the HET track. Read the terrible details Read the terrible details here.