Marquardt-Levenberg fit to a generic function. More...
Public Member Functions | |
| LMFit (const TFUNC &func, const int itermax=1000, const TPAR tol=1e-7, const FVector< bool, NPAR > ignin=false, const TPAR astart=1e-3, const TPAR astep=10.0) | |
| Construct class with fit constraints. More... | |
| void | setIgnore (const FVector< bool, NPAR > &ignin) |
| specify which parameters to leave constant during fit [ignin(i)=true]. More... | |
| FVector< TPAR, NPAR > | getResult () |
| Return result vector. More... | |
| double | getChiSquare () const |
Return final 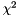 . More... . More... | |
| int | getNIteration () const |
| Return No needed iterations. More... | |
| FVector< TPAR, NPAR > | getVariance () |
| Return diagonal of covariance matrix. More... | |
| FMatrix< TPAR, NPAR, NPAR > | getCovarianceMatrix () |
| Return diagonal of covariance matrix. More... | |
| FVector< TPAR, NPAR > | getErrors () |
| Return the formal errors of the fit parameters. More... | |
| template<typename TDATAX , typename TDATAY > | |
| void | eval (const TDATAX &x, const TDATAY &y, const TDATAY &dy2, const typename TDATAY::value_type nan_y, const FVector< TPAR, NPAR > &inpar) |
Fit to data and 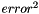 ignoring nan, start with inpar. More... ignoring nan, start with inpar. More... | |
Detailed Description
template<typename TFUNC, typename TPAR, int NPAR, typename Solver = GaussJ<TPAR,NPAR>>
class ltl::LMFit< TFUNC, TPAR, NPAR, Solver >
Marquardt-Levenberg fit to a generic function.
Class to fit an arbitrary function to data and errors by non-linear least squares using the Marquardt-Levenberg algorithm. Either Gauss-Jordan or LU decomposition can be used to solve linear systems during fitting, controlled by a template parameter.
The function object should provide a typedef of value_type and
. Using TPAR to denote the type of the parameters, NPAR their number, and T the type of the argument:
Here's an example class that fits a quadratic function:
This function is used in the following way:
About any container can be used for passing X, Y, and dY data, as long as the container provides
,
,
is the same as the type of the first argument to operator() of the function to be fit. For example, this might well be
, and the container an
to fit a function of 2 variables (and N parameters). This might be a polynomial with crossterms.
Constructor & Destructor Documentation
|
inline |
Construct class with fit constraints.
Member Function Documentation
|
inline |
specify which parameters to leave constant during fit [ignin(i)=true].
References ltl::anyof().
| void ltl::LMFit< TFUNC, TPAR, NPAR, Solver >::eval | ( | const TDATAX & | x, |
| const TDATAY & | y, | ||
| const TDATAY & | dy2, | ||
| const typename TDATAY::value_type | nan_y, | ||
| const FVector< TPAR, NPAR > & | inpar | ||
| ) |
Fit to data and 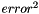 ignoring nan, start with inpar.
ignoring nan, start with inpar.
|
inline |
Return result vector.
|
inline |
Return final 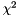 .
.
|
inline |
Return No needed iterations.
|
inline |
Return diagonal of covariance matrix.
References ltl::FMatrix< T, M, N >::traceVector().
|
inline |
Return diagonal of covariance matrix.
|
inline |
Return the formal errors of the fit parameters.
References ltl::FMatrix< T, M, N >::traceVector().
 1.8.5
1.8.5