|
3. ELLIPSOIDS: BULGES, ELLIPTICAL GALAXIES, AND GLOBULAR CLUSTERS
3.1 Surface Photometry
- Review of techniques (photographic,CDD)
- Radial brightness profiles:
- Systematics
- Analytic fitting functions
- D galaxies: properties of cD halos
- Cores: ground-based and HST observations
3.2 Families of Ellipsoidal Stellar Systems
- Global and core parameter correlations
- Three kinds of stellar systems: bulges + ellipticals, Sphs, globulars
- Relationship between Sph and S + I galaxies: Introduction
3.3 The Fundamental Plane of Elliptical Galaxies
- Global and core parameter correlations
- Scalar virial theorem; derivation of the fundamental plane equations
- Implications for galaxy formation; M/L (L )
3.4 Stellar Dynamics:Observations
- Measurement techniques:
- cross-correlation,Fourier quotient,Fourier correlation quotient,...
- Line-of-sight velocity distributions (LOSVDs)
- Observations of rotation and velocity dispersion pro •les
- Velocity anisotropy: the
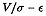 diagram diagram
- Observational confirmation of triaxiality and anisotropy:
- Minor-axis rotation
- Shapes of E galaxies:statistics of apparent shapes
- Isophote twists
- Dust rings:implications for E shapes
3.5 Isophote Shapes:Boxy and Disky Es
- Measurements of isophote shapes: a (4)/a
- Correlations of a (4)/a with physical properties
- Physical dichotomy of E galaxies into
- (1)High-L , nonrotating, boxy, anisotropic Es with cuspy cores, and
- (2)Medium-and low-L , rotating, disky, approximately isotropic and coreless Es
- Proposed revision of the Hubble sequence: boxy E –disky E –S0 –Sa –Sb –Sc –...–Im
- Exceptions: Boxy bulges and low-L boxy Es: origin
3.6 Collisionless Dynamics: Theory
- Stellar systems are fundamentally more complicated than gases:
- Characteristic times: crossing time; relaxation time
- Distribution function
- Fundamental equations of macroscopic stellar dynamics:
- Collisionless Boltzmann equation
- Poisson equation
- First moment equations =basic equations of stellar hydrodynamics:
- Second moment equations: tensor virial theorem
- Application to
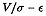 diagram ==> anisotropy diagram ==> anisotropy
3.7 Galaxy Models. I. f =f (E, Lz )
- Jeans Theorem
- Models with f =f (E ):polytropes,isothermals,King models
- Emphasize:similarities between stellar dynamical and gas case (i.e.,stars)
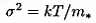
- Core mass-to-light ratios
- Models with f =f (E,Lz )
3.8 Globular Cluster Observations and Models
- Density distributions
- Velocity dispersion profiles
- Models with a range of stellar masses m
3.9 Stellar Orbits in Ellipsoidal Stellar Systems
- Orbits in a spherical potential
- Orbits in axisymmetric potentials: classical integrals
- Orbits in triaxial potentials
3.10 Galaxy Models.II.Galaxy =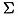 weighti orbiti weighti orbiti
- Schwarzschild ’s method; examples
- Spherical maximum entropy models; examples
- Axisymmetric maximum entropy models; examples
3.11 Dynamical Evolution of Ellipticals and Globular Clusters: Theory
- Phase mixing and violent relaxation
- Origin of the
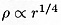 density distribution density distribution
- Two-body encounters and relaxation
- Heat capacity of a self-gravitating stellar system is negative
- Core collapse: single-
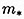 simulations simulations
- Stopping core collapse via binaries
- Gravothermal oscillations
- Complications: range of
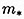 , primordial binaries, stellar evolution, physical stellar collisions, stellar coalescence, runaway stellar mergers,... , primordial binaries, stellar evolution, physical stellar collisions, stellar coalescence, runaway stellar mergers,...
- External influences:
- Tidal effects
- Disruption of globular clusters by galactic disk shocking
- Relation between present and primordial globular cluster population
3.12 Dynamical Evolution of Ellipticals and Globular Clusters: Observations
- Post-core-collapse density distributions in globulars
- Mass segregation
- Stellar population gradients:blue stragglers
- Stellar population gradients in bulges and Es <== effects of high stellar density
3.13 Supermassive Black Holes (BHs)in Galactic Nuclei
- Brief motivation: nucelar activity (see §9)
- Origin of seed BHs via evolution of dense stellar systems
- Stellar-dynamical search for BHs
- Gas-dynamical search for BHs
- BH demographics
- Flashes when stars are accreted by BHs
|