In the early days of xyfitter I was using it to fit polynomials to marginal distributions. Beacuse the row/column values in such data sets can be quite large numbers, it is very important to normalize the X data to a smaller range. Here I show a few files used and command lines for makeing the plot at the bottom.

xyfitter margdist_sub pixel mean poly7 N  

% cat X.normit 
180.0  15.0 

% cat margdist_sub.parlab 
pixel   Row Number
mean    Mean signal value (adu) 
sig     Standard devistion (adu) 
me      Mean error about mean (adu) 
Npix    Number of pixels 

% cat margdist_sub.table 
# row averaged marginal distribution 
# data
 187.0     2507.3071      74.0778      12.1783       37.0
 188.0     2551.4509     117.7900      19.3645       37.0
 189.0     2602.8206     194.9535      32.0502       37.0
 190.0     2701.8748     300.9678      49.4788       37.0
 191.0     2813.3882     491.4593      80.7954       37.0
 192.0     2990.6313     737.1098     121.1801       37.0
 193.0     3258.0732    1111.2894     182.6949       37.0
 194.0     3529.5684    1574.3077     258.8146       37.0
 195.0     3835.0820    2043.3593     335.9262       37.0
 196.0     4001.7227    2340.0701     384.7051       37.0
 197.0     4051.6040    2460.2288     404.4591       37.0
 198.0     3932.4873    2253.2725     370.4357       37.0
 199.0     3677.1541    1835.4631     301.7483       37.0
 200.0     3363.3704    1320.0219     217.0103       37.0
 201.0     3083.9011     889.3854     146.2141       37.0
 202.0     2892.8655     555.6920      91.3552       37.0
 203.0     2740.6313     342.7261      56.3438       37.0
 204.0     2637.1086     219.9106      36.1531       37.0
 205.0     2574.2351     137.5822      22.6184       37.0

% cat Axes.20  
Poly fits using X normalization 
  187.00000 205.00000 Row Number 
  2507.30710 4051.60400 Mean signal value (adu) 

% cat List.20 
margdist_sub.table  1 2 0 0   point  r o 100  Obs
poly3.fitcurve      1 2 0 0   line   b - 10   poly3 
poly4.fitcurve      1 2 0 0   line   c - 10   poly4 
poly5.fitcurve      1 2 0 0   line   g - 10   poly5 
poly7.fitcurve      1 2 0 0   line   m - 10   poly7 

% xyplotter List.20 Axes.20 

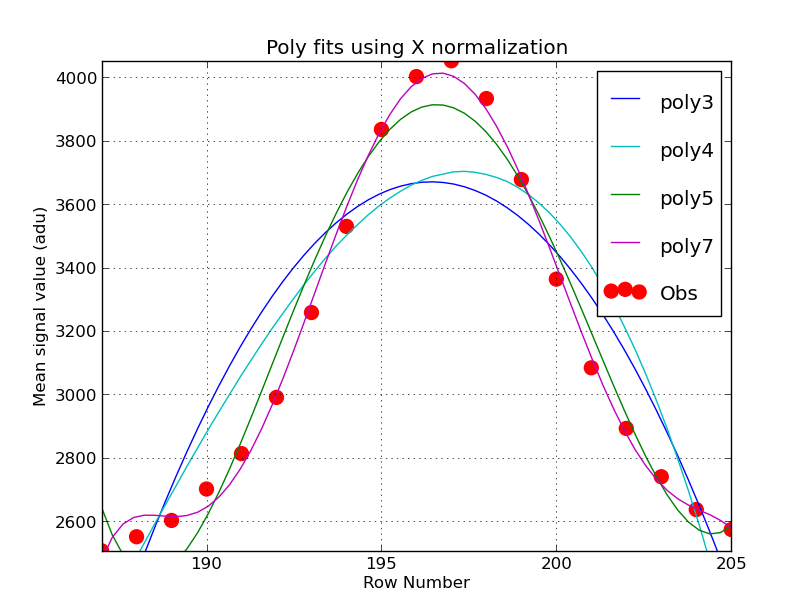
An example of polynomial fitting to data from clip_margdist.sh. The X data (Row values in pixel units) were averaged using the normit.sh routine in order to avoid sever round-off error. The data are very peaky, so a k=7 term polynomial gives the best estimate to the [center,peak] values.